RWA1: Unit M Concept 5: Ellipses

1) Mathematical Definition:"A curved line forming a closed loop, where the sum of the distances from two points (foci) to every point on the line is constant." (http://www.mathopenref.com/ellipse.html)

2) Description:
Algebraically: (http://imanawkwardturtle.files.wordpress.com/2013/03/hyperbolas3.png)
The two equations above produce an ellipse. If the "a" value is under the x, then that would give you a horizontal/fat ellipse. If the "a" value is under the y, then that will give you a vertical/skinny ellipse.

Graphically: 
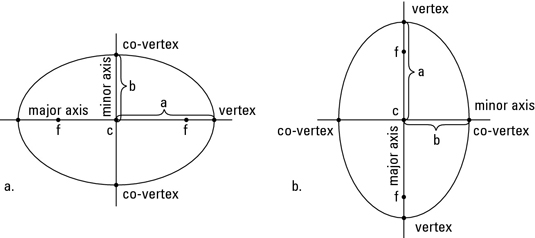
(http://www.dummies.com/how-to/content/how-to-graph-an-ellipse.html)
An ellipse is basically a circle that has been squished either horizontally or vertically.
Key Features:
It consists of a center, a major axis, 2 vertices, a minor axis, and 2 co-vertices. The foci are pretty important. They are the two points that tell you how fat of how skinny the ellipse is. They are always located on the major axis. The eccentricity for an ellipse must be bigger than 0 but less than 1. To find it, you simply divide "c" by "a".
3) Real World Applications: 
(http://www.skooolnigeria.com/studyuploadedimages/planetsNoPluto.gif)
The orbits of these planets are ellipses. As you can see in this picture, you can see the orbit that that planet takes when its going around the earth. This is a good example of an ellipse. Below is another great visual :)

4) References:
(http://www.mathopenref.com/ellipse.html)
(http://imanawkwardturtle.files.wordpress.com/2013/03/hyperbolas3.png)
(http://www.dummies.com/how-to/content/how-to-graph-an-ellipse.html)
(https://www.youtube.com/watch?v=WqezXu2U_OI)

BQ #6: Unit U: Concepts 1-8

BQ#4 Unit T: Concept 3 Tangent and Cotangent Graphs

"Why is a “normal” tangent graph uphill, but a “normal” COtangent graph downhill? Use unit circle ratios to explain."

The reason for this is that both tangent and cotangent have asymptotes in different places on their graph due to the fact that they have different ratio identities. Tangent has cosine in the bottom and cotangent has sin in the bottom. When you look at the pictures below, you can see the differnece between the two graphs, the asymptotes are in different places.

 y=tan(x)

http://www.regentsprep.org/Regents/math/algtrig/ATT7/othergraphs.htm

Ratio for Tangent is: sin/cosine

Asymptotes will happen when cosine equals to zero.

 y=cot(x)

http://www.regentsprep.org/Regents/math/algtrig/ATT7/othergraphs.htm

Ratio for cotangent is: cosine/sin
Asymptotes happen when sin equals to zero.

http://www.regentsprep.org/Regents/math/algtrig/ATT7/othergraphs.htm

BQ #3: Unit T: Concepts 1-3

How do the graphs of sine and cosine relate to each of the others?  Emphasize asymptotes in your response.

Tangent?
We draw asymptotes by looking at cosine. Ratio for tangent is sin/cos. The asymptotes for tangent is undefined because cos has to be equal to 0 in order for it to be undefined. Every time Cos hits the x-axis, we draw an asymptote. Tangent has a period of pi, and it is positive, negative, positive, negative.

Cotangent?

Here, we draw the asymptotes by looking at sin. Ratio for cotangent is cosine/sin. Every time Sin hits the x-axis, we draw an asymptote. It too has a period of pi.

Secant?

For this one, we draw asymptotes looking at cosine again because it is the reciprocal. Ratio is 1/cosine. For Cosine, we draw the asymptotes when cos=0 or it crosses the x-axis.

Cosecant?

We look at sin to draw the asymptotes because it is the reciprocal. Ratio is 1/sin. When sin=o, that gives us the asymptotes.

BQ#5: Unit T Concept 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

-Sin and Cosine do not have asymptotes because they can never be undefined. Both have a denominator of "r" which always is qual to 1. The only way to get undefined values in ratios is to have a denominator of zero. For Cosecant, Secant, Tangent, and Cotangent, those have asymptotes because its possible for them to have a zero as the denominator unlike Sin and Cosine.

BQ#2: Unit T Concept 1 Intro: Trig Graphs and Unit Circle

1) How do Trig Graphs relate to the Unit Circle?
Period? - Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

We use ASTC, and as you can see in this picture, i've labeled them already. For Sine, it is ++--, and i give a little visual in the bottom. For Cosine, it is +--+ and i too put another visual. For Tangent/Cotangent, it is +-+-, and this one is different from the other two, because it only take pi to make a period/revolution as the other two took 2pi, to make the period/revolution..


Amplitude? – How does the fact that sine and cosine have amplitudes of one (and the other trig functions don’t have amplitudes) relate to what we know about the Unit Circle?

Sine and Cosine are the only two that have r as the denominator. r=1. Therefore, they cant be bigger than 1.

Reflexion #1- Unit Q: Verifying Trig Identities

1. What does it actually mean to verify a trig identity?
Verifying an identity means to make whatever you have equal to one of the identities we are given such as the reciprocal identities or the pythagorean identities. We also use the unit circle to help us too.
2. What tips and tricks have you found helpful?
When Mrs.Kirch suggested making those flashcards, that helped me most because without them, i wouldn't have memorized the identities we are supposed to.

3.Explain your thought process and steps you take in verifying a trig identity.  Do not use a specific example, but speak in general terms of what you would do no matter what they give you. You have to see if the problem that is given to you can match up to one of the identities. You use them along the problems to either simplify them, or make them smaller.

SP #7: Unit Q Concept 2: Finding All Trig Functions Using Identities

“Please see my SP7, made in collaboration with Eldon, by visiting their blog here.  Also be sure to check out the other awesome posts on their blog”

I/D #3:Unit Q Concept 1:Pythagorean Identities

Inquiry Activity Summary:

An identity is a proven fact or formula that is always true. We will be showing you how the pythagorean theorem is an "identity" in my work below:

-Finding: (Sin^2x+Cos^2x=1)
-Pythagorean Theorem: x^2+y^2=r^2
-Sin=y/r; Cos=x/r
-Substitute the trig functions into the pythagorean theorem:
(y/r)^2+ (x/r)^2= 1
-equals the same thing as saying Sin^2x+Cos^2x=1
-We can then check it by lets say, using the 45degree angle in our Unit Circle.
-Coordinates are (rad2/2, rad2/2)
                               x          y
-(rad2/2)^2+ (rad2/2)^2=1
-The radical in rad2 cancels, you square the 2 in the bottom and your left with
-(2/4)+(2/4)=1
-(4/4)=1
-Correct!

Inquiry Activity Reflection:

-The connections that i see between Units N, O, P, and Q so far are that they all have something to do with the unit circle, we have to derive stuff.
-Three words that I would describe trigonometry would be fascinating, hard, but doable.

WPP #13 & 14: Unit P Concept 6 & 7

Please see my WPP13-14, made in collaboration with Clyde, by visiting their blog here  Also be sure to check out the other awesome posts on their blog.

WPP #12: Unit O Concept 10: Angle of Elevation and Depression Word Problems

Part 1: Three Year Old Jake sees a cookie jar on top of the fridge. The angle of elevation from the ground in 29 degrees. The distance from Jake to the fridge id 12 feet. What is the height of the cookie jar on top of the fridge? (round to the nearest tenths place).

Part 2: After he successfully gets the cookie jar on top of the fridge, he spots his favorite little super awesome toy car. The height of the fridge would be ___ (Have to find the first part). The angle of depression is 32 degrees. What id the distance from Jake to his favorite little super awesome toy car?

Part 1

Part 2